Growing your wealth exponentially with compounding

Most Americans are taught the math to calculate compound interest in primary school yet almost none of them understand why the heck it matters to them. That's a shame, because compounding can determine whether you reach your financial goal (whether that goal is supporting your family, retiring early, founding a start-up, buying a boat, or something else).

What is compound interest? To explain it clearly, we'll cover the three components of earnings, in order: savings, simple interest, and compound interest.

Component #1: Savings

Savings are the dollars you sack away from your compensation after your expenses are paid. Let's say a project manager is paid $100,000 per year and spends $50,000 on living expenses. The remaining $50,000 represents their savings.

The thing about savings is that they are unlikely to grow significantly over time. Sure, if our project manager applies themself, they'll get promotions and raises every few years. But realistically, savings won't increase much because an employee can't expect consistent growth or huge leaps in compensation.

Accumulating savings is like picking apples. You may be able to get a bigger basket, or find an apple-farm where the trees are easier to harvest. But if you want more apples every year, you'll have to drive out to the farm, put in the effort, and pick the apples.

What does this mean to you? The amount you save will be directly proportional to the length of time you work. If you never invest, even if you're "rich" in compensation, you need to keep working day in and day out just to keep your account growing constantly.

Component #2: Simple interest

Simple interest is the money you earn by investing your savings. Simple interest is likely to grow super-linearly over your career, meaning you'll make more money from interest each year. This is because your return on investment (in our example, 8.73%) will be roughly constant over time¹ but the amount of savings accumulating in your bank account will be increasing every year.

For example, let's take a look at the simple interest the grad in the previous post made:

Year	This year's savings	Total savings (excluding interest)	This year's simple Interest
1	$60,000	$60,000	8.73% * $60,000 = $5,238
2	$60,000	$120,000	8.73% * $120,000 = $10,476
3	$60,000	$180,000	8.73% * $180,000 = $15,714

You can see how the money the grad makes from simple interest each year increases as their savings grow. This acceleration of additional earnings is exciting -- they'll represent more than 20% of the grad's yearly wages by their 6th year on the job. That's like getting paid for Saturday every week without working!

But compound interest will actually grow even faster.

Component #3: Compound interest

Compound interest is the money you earn by investing your simple interest. It sounds confusing but let's unpack it.

In the table above, the grad earned $5,238 in simple interest after Year 1 by investing $60,000 of savings. Well, imagine if they took that $5,238 and immediately re-invested it. The next year, they would have earned an extra 8.73% * $5,238 = $457. That $457 is the compound interest.

It may seem like a measly sum, but then they'll take that $457 and re-invest it along with the additional simple interest they earn. The following year, they'll earn $1,412 of compound interest which they'll reinvest again.

By repeating this process over and over, we'll see exponential growth that is astonishing. By year 30, this $457 of compound interest earned from the first year will have snowballed into $3.7 million, accounting for 48% of their total wealth. In an apocryphal story, even Albert Einstein was impressed and called compound interest "the most powerful force in the universe".²

An exponential rodent infestation

If you're not familiar with compounding, this might seem hard to believe. You'd be in good company, because exponential growth is notoriously unintuitive. Humans are good at estimating constant growth without thinking (if I keep picking 5 apples at the same rate, how long will it take to fill my basket?). Humans are bad at estimating exponential growth.

One analogy that gives an intuition for compounding is reproducing mice. Think of a pair of mice (a male and a female) sitting in the corner of your kitchen. As mice tend to do, they start to mate. A few weeks later, the baby mice arrive (mice have 7 children per litter on average³). Before you know it, several generations of mice are growing up in your kitchen, with each successive generation having their own children (first 7, then 21, then 70, then 245, then 854). If I tell you that each female mouse can have 5-10 litters per year, you'll quickly realize you have an exponentially growing rodent infestation -- there will be over 179,000 mice by just the 10th generation.

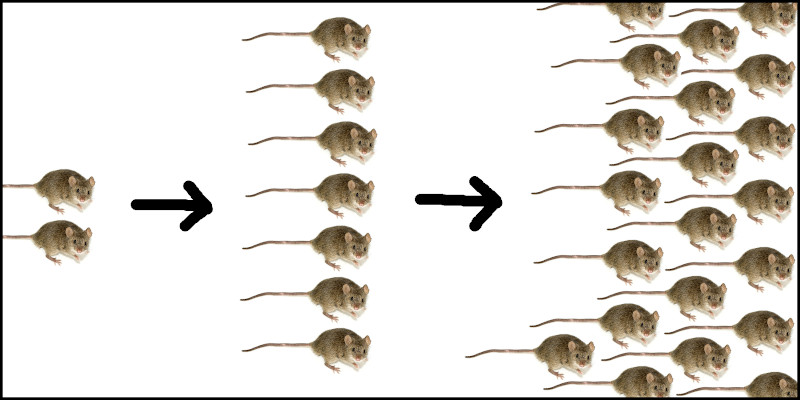
Compounding is the exponential "reproduction" of money, caused by repeatedly reinvesting money you have just earned from investing. Dollar 1 returns dollar 2; then dollar 1 and 2 each return dollar 3 and 4; and so on. Compounding interest from the stock market doesn't grow as fast as mice reproduce, but it grows plenty fast to change your life.

Take a look at this graph showing how much of our grad's nest-egg has come from each component of wealth of the years. Enter your own inputs in the form next to the graph to see how compounding might grow your wealth over time:

This graph should match up with what you learned over the course of this post:

1. Savings grow linearly (in proportion to how much you work)
2. Simple interest grows super-linearly (in proportion to the size of your savings)
3. Compound interest starts out small, but grows exponentially (in proportion to the savings + simple interest).

The graph also hints at why it's so difficult to get people to pay attention to basic personal finance. Savings is the only visible component for the first 10 years. The compound interest line is only visible after 15 years. Few people have the patience to save diligently for years, for future benefit. But in this example, after 30 years, the grad will be 4x richer due to investing. Patience pays.

Another useful way to view the different components of wealth is by the percentage of your account balance that it holds over time. Again, enter your own inputs in the form next to the graph to see how your own components would look:

In this graph, it's even clearer that, over time, investment returns (simple interest plus compound interest) will become an important, and later a dominating factor of wealth. Somewhere around Year 16, more than 50% of the nest-egg will have come from investment returns. By year 24, compound interest has earned more money than either savings or simple interest due to the exponential growth.